1)      Czym jest korelacja?:

 

A)            Wzajemnym oddziaływaniem dwóch zjawisk w tej samej zbiorowości

 

B)      Wzajemnym brakiem oddziaływania zjawisk na siebie

 

C)      Brakiem oddziaływania pierwszego zjawiska na drugie

 

D)     Brakiem oddziaływania drugiego zjawiska na pierwsze

 

2)      Liczby względne to:

 

a)      Suma liczb bezwzględnych

 

b)             Iloraz liczb bezwzględnych

 

c)       Iloczyn liczb bezwzględnych

 

d)      Różnica liczb bezwzględnych

 

3)      Wskaźnik natężenia stanowi:

 

a)      Stosunek wielkości dwóch zbiorowości będących ze sobą w logicznym związku

 

b)       Różnica wielkości dwóch zbiorowości będących ze sobą w logicznym związku

 

c)       Suma wielkości dwóch zbiorowości będących ze sobą w logicznym związku

 

d)      Iloczyn wszystkich zbiorowości będących ze sobą w logicznym związku

 

4)      Miarą klasyczną jest:

 

a)      Kwantyl

 

b)      Dominanta

 

c)       Mediana

 

d)             Średnia kwadratowa

 

5)      Metoda opisowa charakteryzuje się:

 

a)      Przedstawieniem danych w postaci tablic statystycznych

 

b)      Przedstawieniem danych w postaci wykresów statystycznych

 

c)             Przedstawieniem danych w postaci tekstu mającego charakter opisu statystycznego

 

d)      Zastosowaniem kilku metod prezentacji danych

 

6)      Graficzna prezentacja danych statystycznych składa się z:

 

a)             Tytułu, pola wykresu, legendy, źródła danych

 

b)      Pola wykresu, legendy, tabeli, źródła danych

 

c)       Tytułu, pola wykresu, źródła danych, danych roboczych

 

d)      Tytułu, pola wykresu, legendy, opisu wykresu

 

 

 

 

 

 

 

7)       Zbiorowości NIE dzielimy ze względu na:

 

a)      Ilość jednostek

b)      Rodzaj potrzeb

 

c)       Cechę zbiorowości

 

d)             Przynależność terytorialną

 

8)      Zbiorowość klasyczna składa się z:

 

a)             Jednostek, które istniały, istnieją lub będą istnieć w ściśle określonym momencie czasu

 

b)      Jednostek, które istniały, istnieją lub będą istnieć w każdym momencie czasu

 

c)       Jednostek, które istniały, istnieją lub będą istnieć w całym przedziale czasowym poza jednym określonym punktem w momencie czasu

 

d)       Jednostek, które istniały, istnieją lub będą istnieć w kilku punktach momentu czasu

 

9)      Definicja nie wchodząca w skład definicji cech mierzalnych to:

 

a)        Zmienność skokowa

 

b)      Zmienność ciągła

 

c)       Zmienność quasi ciągła

 

d)             Zmienność rozłączna

 

10)   Materiał statystyczny można podzielić na następujące rodzaje:

 

a)      Pierwotny

 

b)      Wtórny

 

c)       Surowy

 

d)             nieprzypisany

 

11.  Która z tablic gromadzi surowy materiał statystyczny, który podlega dalszej "obróbce":

 

a)  Wynikowa

 

b)  Robocza

 

c)  Prosta

 

d)  Złożona

 

12.  Dobierz jednostkę do próby gdy znany jest podział zbiorowości na mniejsze grupy według kryteriów mających związek z badaniem statystycznym:

 

a)  Proporcjonalny

 

b)  Losowy

 

c)Celowy

 

d)Przez eliminację

 

13.  Która metoda przedstawia dane w postaci wykresów statystycznych

 

a)  Tabelaryczna

 

b)  Opisowa

 

c)  Mieszana

 

d)  Graficzna

 

14.  W jaki sposób wykonujemy obliczenia dla każdej jednostki terytorialnej wartości badanego zjawiska i zabarwieniu lub zakreskowaniu jej powierzchni w odpowiedniej skali:

 

a)  Metoda figur geometrycznych

 

b)  Metoda obrazkowa

c)  Metoda powierzchniowa

 

d)  Metoda ilościowa

 

15.  Wskaźnik natężenia to:

 

a)  Stosunek wielkości dwóch zbiorowości będących ze sobą w logicznym związku

 

b)  Liczbowa ilustracja udziału poszczególnych części danej zbiorowości

 

c)  Stosunek wielkości dwóch zbiorowości nie będących ze sobą w logicznym związku

 

d)  Stosunek dwóch zbiorowości przedstawionych liczbowo

 

16.  Niepoprawny sposób wyznaczania średniej arytmetycznej:

 

a)  średnia arytmetyczna zwykła - dla indywidualnego wykazu wartości

 

b)  średnia arytmetyczna wyrażona za pomocą częstości odchyleń

 

c)  średnia arytmetyczna wyrażona za pomocą wzoru kumulacyjnego

 

d)  średnia arytmetyczna ważona - dla szeregu rozdzielczego przedziałowego

 

17.  Korelacja jest to:

 

a)  wzajemne oddziaływanie dwóch zjawisk tej samej zbiorowości.

 

b)  wzajemne oddziaływanie dwóch zjawisk rożnej zbiorowości.

 

c)  wzajemne oddziaływanie kliku zjawisk z różnych zbiorowości.

 

d)  wzajemne oddziaływanie zbiorowości na określone zjawiska

 

18.  Która z podstawowych metod nie opisuje współzależności zjawisk:

 

a)  porównawcza

 

b)  opisowa

 

c)  graficzna

 

d)  tabelaryczna

 

19.  Przyrost absolutny:

 

a)  pozwala nam porównać dwie wielkości wyrażone w tych samych jednostkach

 

b)  pozwala nam porównać dwie wielkości wyrażone w różnych jednostkach

 

c)  najczęściej używamy go do porównania wielkości zjawisk w okresach nie następujących po sobie

d)  pozwala nam porównać kilka wielkości wyrażonych w różnych jednostkach

 

20.  Średnia arytmetyczna jest:

 

a)  ilorazem zsumowanych wartości występujących u po szczególnych jednostek badanej zbiorowości przez liczbę tych jednostek

 

b)  iloczynem zsumowanych wartości występujących u po szczególnych jednostek badanej zbiorowości przez liczbę tych jednostek

 

c)  iloraz wielkości badanej zbiorowości przez sumę wartości po szczególnych jednostek

 

d)  iloczynem wielkości badanej zbiorowości przez sumę wartości po szczególnych jednostek

 

 

 

1.  Miary pozycyjne to:

 

a)             średnia arytmetyczna, średnia geometryczna, dominanta, średnia kwadratowa

 

b)             średnia arytmetyczna, mediana, dominanta

 

c)             kwantyle, mediana, dominanta

 

d)             dominanta, średnia arytmetyczna

2.  Zbiorowość składająca się z jednostek, które istniały, istnieją lub będą istnieć w pewnym przedziale czasu to zbiorowość:

 

a)              skończona

 

b)              statyczna

 

c)              nieskończona

 

d)     dynamiczna

 

3.  Wybierz prawidłową kolejność wykonywania poszczególnych etapów badania statystycznego:

a)             przygotowanie badania, zebranie materiału statystycznego i przygotowanie do opracowania, opracowanie materiału statystycznego, prezentacja danych statystycznych, analiza statystyczna.

 

b)             przygotowanie badania, zebranie materiału statystycznego i przygotowanie do opracowania, analiza statystyczna, opracowanie materiału statystycznego, prezentacja danych statystycznych.

 

c)              zebranie materiału statystycznego i przygotowanie do opracowania, opracowanie materiału statystycznego, przygotowanie badania, prezentacja danych statystycznych, analiza statystyczna.

 

d)     przygotowanie badania, zebranie materiału statystycznego i przygotowanie

 

do opracowania, opracowanie materiału statystycznego, analiza statystyczna, prezentacja danych statystycznych.

 

4.  Którą z tablic można opisać słowami: Gromadzi surowy materiał statystyczny, który podlega dalszej „obróbce”?

a)             Tablica prosta

 

b)             Tablica złożona

 

c)             Tablica robocza

 

d)     Tablica wynikowa

 

5.  Metoda graficzna przedstawiania danych statystycznych to:

 

a)      przedstawienie danych w postaci tablic statystycznych

 

b)      przedstawienie danych w postaci wykresów statystycznych

 

c)       przedstawienie danych statystycznych w postaci tekstu mającego charakter opisu statystycznego

 

d)             zastosowanie kilku metod prezentacji danych

 

6.  Elementy każdego wykresu to (może być kilka poprawnych odpowiedzi):

 

a)             tytuł

 

b)             pole wykresu

 

c)             legenda

 

d)             źródło danych

 

7.  Metoda symbolowa

 

a)             polega na umieszczeniu w polu mapy symboli wyrażających badane zjawisko. Liczba symboli jest proporcjonalna do wielkości zjawiska dotyczącego danego terytorium.

 

b)             polega na obliczeniu dla każdej jednostki terytorialnej wartości badanego zjawiska i zabarwieniu lub zakreskowaniu jej powierzchni w odpowiedniej skali.

c)              polega na tym, że na mapie umieszczamy punkty, których liczba jest proporcjonalna do wielkości badanego zjawiska występującego na danym terytorium.

 

d)             polega na umieszczeniu figur geometrycznych ( najczęściej prostokątów, kół itp. ) w odpowiednich miejscach mapy geograficznej w zależności od występowania badanego zjawiska. Pole powierzchni figury jest uzależnione od wielkości zjawiska, a wyodrębnione części tej figury są proporcjonalne do części obrazującej strukturę zbiorowości na tym terenie.

8.   wzór ten opisuje:

 

a)             średnią arytmetyczną ważoną - dla szeregu rozdzielczego punktowego

 

b)             średnią arytmetyczną ważoną - dla szeregu rozdzielczego przedziałowego

 

c)              średnią arytmetyczną wykorzystującą metodę odchyleń dla szeregu indywidualnego

 

d)             średnią arytmetyczną wyrażoną za pomocą wzoru kumulacyjnego

 

9.  Miary odchylenia pozycyjne to:

 

a)      odchylenie przeciętne, standardowe, klasyczny współczynnik zmienności i obszar wartości typowych

 

b)      odchylenie ćwiartkowe, standardowe, klasyczny współczynnik zmienności i obszar wartości typowych

 

c)      rozstęp, odchylenie ćwiartkowe, pozycyjny współczynnik zmienności i obszar wartości typowych

 

d)             pozycyjny współczynnik zmienności, odchylenie ćwiartkowe, standardowe i obszar wartości typowych

 

10.  Zadania statystyki :

 

a)             wnioskowanie statystyczne, przechowywanie danych statystycznych, analiza statystyczna

 

b)             gromadzenie danych statystycznych, analiza statystyczna, informacja statystyczna

c)              wnioskowanie statystyczne, informacja statystyczna, gromadzenie danych statystycznych

 

d)             wnioskowanie statystyczne, informacja statystyczna, analiza statystyczna

 

 

 

 

 

 

 

11.  „Jeśli dokonujemy k wyborów, przy czym dla pierwszego z nich mamy m1 możliwości, dla drugiego - m2 , ...., dla ostatniego mk możliwości, to wszystkich możliwości wyborów jest m1 ·

m1 · ... · mk”. Zdanie to jest definicją:

 

a)      reguły dodawania

 

b)      prawa de Morgana

 

c)      reguły mnożenia

 

d)     zbioru uniwersalnego

 

12. Kolejność nie jest ważna w przypadku:

a)      kombinacji

 

b)      permutacji

 

c)      wariacji

 

d)     żadna z odpowiedzi nie jest poprawna

 

13.  Analiza dynamiki ustala:

 

a)      poziom wzrostu, lub spadku badanego zjawiska

 

b)      tylko aktualny poziom badanego zjawiska

 

c)      czy dane zjawisko występuje

 

d)     opłacalność tworzenia danego produktu

 

14.  Przyrost względny jest to:

 

a)      wielkość zjawiska z okresu podstawowego

 

b)      wielkość zjawiska z okresu badanego

 

c)      iloraz przyrostu absolutnego przez wielkość zjawiska z okresu podstawowego.

 

d)     przyrost będący zawsze dodatnim

 

15.  Kiedy korelacja jest ujemna:

 

a)      kiedy zmiany obu cech są różnokierunkowe, a więc wzrost wartości jednej cechy powoduje spadek wartości drugiej cechy lub spadek wartości jednej cechy powoduje wzrost drugiej

 

b)      kiedy zmiany obu cech są jednokierunkowe, a więc wzrost wartości jednej cechy powoduje wzrost wartości drugiej cechy lub spadek wartości jednej cechy powoduje spadek drugiej

 

c)      kiedy obie cechy są zawsze ujemne

 

d)     kiedy obie cechy są zawsze dodatnie

 

16.  Podstawowe metody opisu współzależności zjawisk to (może być kilka poprawnych odpowiedzi):

 

a)      kartogramowa

 

b)      porównawcza

 

c)      graficzna

 

d)     tabelaryczna

 

17.  Co to jest korelacja:

 

a)      dominanta z dwóch, lub więcej zjawisk

 

b)      dwa, lub więcej przypadkowych zjawisk

 

c)      wzajemne oddziaływanie dwóch zjawisk z przypadkowych zbiorowości

 

d)     wzajemne oddziaływanie dwóch zjawisk tej samej zbiorowości

 

18.  Jakie kroki należy wykonać, żeby dokonać porównania ilościowego odpowiadających sobie właściwości dwóch lub więcej zbiorowości statystycznych:

 

a)      wyznaczyć wartości odpowiednich miar statystycznych

 

b)      przeprowadzić analizę przedmiotową (interpretacja otrzymanych wyników)

 

c)      ocenić wyniki pod względem dokładności i wiarygodności

 

d)     wszystkie odpowiedzi są poprawne

19.  Tabelaryczną formę prezentacji możemy podzielić na:

 

a)      szeregi i tablice

 

b)      diagramy i szeregi

 

c)      diagramy i kartogramy

 

d)     szeregi i wykresy

 

20.  Jednostka statystyczna to:

 

a)      jednostka z układu SI

 

b)      element zbiorowości statystycznej będący przedmiotem badania statystycznego

 

c)      grupa elementów zbiorowości statystycznej będąca przedmiotem badania statystycznego

 

d)     jednostka oddający przeciętny stan aktualnie badanego zjawiska

 

1.  Która z podanych grup cech należy do cech mierzalnych? A) Przestrzenna

 

B) Zmienna skokowa C) Czasowa

D) Rzeczowa

 

2.  Która z wymienionych form prezentacji danych jest niewłaściwa? A) Opisowa

 

B) Graficzna

 

C) Tabelaryczna

 

D) Linijkowa

 

3.  Która z podanych miar należy do grupy miar klasycznych?

 

A)  Średnia arytmetyczna

 

B)  Mediana

 

C)  Dominanta

 

D)  Kwantyle

 

4.  Kwantyle rzędu 1/4, 2/4, 3/4 nazywane są po prostu kwantylami. Jak nazywamy kwantyle rzędu 1/10, 2/10, …, 9/10 ?

 

A) Kwintyl B) Mediana

 

C) Decyl D) Percentyl

 

5.  Zaznacz wzór na indeks ułamkowy.

 

A)  IOi = xi / x0 ∙ 1000‰

 

B)  IOi = xi / x0

 

C)  IOi = xi / x0 ∙ 100%

 

D)  IOi = xi / xi-1 ∙ 1000‰

 

6. Prawo de Morgana mówi że:

 

A)  (A∩B)’ = A∪B

 

B)  (A∩B)’ = A’∩B

 

C)  (A∩B)’ = A’∪B’

 

D)  (A∩B)’ = A∩B’

 

7.  Zdarzenia elementarne oznaczamy symbolem:

 

A) Ѡi

 

B)  ∅

 

C)  Ω

 

D)  U

 

8.  Wartość występująca najczęściej w rozkładzie empirycznym cechy to: A) mediana

 

B) średnia arytmetyczna C) obszar zmienności

 

D) dominanta

 

9.  Mediana liczb: 1,2,3,5,7,7,8,9 jest równa

 

A)  4

 

B)  5

 

C)  6

 

D)  7

 

10.  Wariancja nigdy nie może być A) dodatnia

 

B) równa zero

 

C) mniejsza od odchylenia standardowego

 

D) ujemna

 

11.  Jak często GUS przeprowadza spis powszechny?

 

A) Raz na 10 lat B) Raz na 5 lat C) Raz na 2 lata D) Raz na 4 lata

 

12.  Jaka z podanych cech nie jest cechą mierzalną? A) Zmienność skokowa

 

B) Zmienność ciągła

 

C) Zmienność Quasi Ciągła

 

D) Zmienność ilościowa

 

13.  Które z podanych zdań jest nieprawdziwe?

 

A)  Średnia arytmetyczna jest wielkością mianowaną

 

B)  Zbiorowość statystyczna jest to zbiór identycznych jednostek

C)  Korelacja jest to wzajemne oddziaływanie dwóch zjawisk tej samej zbiorowości

 

D)  Wynikiem permutacji jest funkcja różnowartościowa określona w zbiorze A

 

14.  Podstawowymi metodami opisu współzależności zjawisk są A) metoda słupkowa, graficzna i tabelaryczna

 

B) metoda graficzna, tabelaryczna i porównawcza C) metoda tabelaryczna, słupkowa i porównawcza D) metoda porównawcza, graficzna i słupkowa

 

15.  Siłę korelacji wyznaczamy korzystając z współczynników korelacji:

 

A) Spearmana i Pearsona B) Spearmana i Paaschego C) Spearmana i Laspeyresa D) Laspeyresa i Paaschego

 

16.  W analizie dynamiki bierzemy pod uwagę:

 

A)  Przyrost absolutny, przyrost względny, przyrost elementarny, tempo wzrostu, średnie tempo dynamiki

 

B)  Przyrost absolutny, przyrost elementarny, tempo wzrostu, średnie tempo dynamiki

 

C)  Przyrost absolutny, przyrost względny, indeksy, tempo wzrostu, średnie tempo dynamiki

 

D)  Przyrost absolutny, przyrost względny, przyrost elementarny, indeksy, średnie tempo dynamiki

 

17.  Który z symboli oznacza zbiór uniwersalny B) Û

C) Ü

 

D) ÚA) U

 

 

 

18)  Współczynnik skupienia (Kurtoza) obliczana jest wzorem:

 

A) K = m4/s4 B) K = m4*s4 C) K = 2*m4/s4 D) K = m4/2s4

 

19)  Zbiór zdarzeń elementarnych nie może być:

 

A)  skończony

 

B)  nieskończony

 

C)  przeliczalny

 

D)  nieprzeliczalny

 

20)  Którego z poniższych warunków nie spełnia lista wyników zdarzenia elementarnego: A) lista wyników musi być kompletna

 

B) elementy listy wyników są parami rozłączne C) elementy listy wyników są nierozkładalne

 

D) Lista wyników musi być skońćzona

 

1.     Która nazwa nie jest nazwą szeregu:

 

a.                       Szereg prosty.

 

b.    Szereg rozdzielczy zagregowany.

 

c.     Szereg rozdzielczy z przedziałami klasowymi.

 

d.     Szereg rozdzielczy punktowy.

 

2.  Średnią harmoniczną:

 

a.                       Stosuje się w badaniach średniego tempa zmian zjawisk, a więc gdy zjawiska są ujmowane dynamicznie. Stosuje się ją dla wartości stosunkowych.

 

b.     Stosuje się wtedy, gdy wartości cechy są podane w przeliczeniu na stałą jednostkę innej zmiennej, czyli w postaci wskaźników natężenia, np. prędkość pojazdu w km/h.

 

c.     Żadna odpowiedź nie jest prawidłowa.

 

d.     Oznacza okresowe tempo wzrostu lub spadku wielkości badanego zjawiska w czasie, przy nie zmieniającej się tendencji rozwojowej

 

 

3.  Średniej arytmetycznej nie należy liczyć gdy:

 

a.                       W szeregu występują wartości nietypowe.

b.     Zbiorowość jest niejednorodna pod względem badanej cechy.

 

c.                       Wszystkie odpowiedzi są poprawne.

 

d.     Pierwszy lub ostatni przedział klasowy jest otwarty.

 

4.  Mediana:

 

a.                       Odpowiedzi c i d są poprawne.

 

b.     Żadna odpowiedź nie jest poprawna.

 

c.     Dzieli zbiorowość na dwie równe części.

 

d.     Zaliczana jest do miar średnich.

 

5.  Statystyczna zależność między dwoma zmiennymi powiązanymi ze sobą w sposób logicznie uzasadniony to:

 

a.                       Kompetacja

 

b.     Panteneum

 

c.                       Korelacja

 

d.     Antracja

 

6.  Jeżeli podczas liczenia złożonego indeksu fizycznej wielkości wolumenu, stały miernik przyjmiemy w wartościach okresu podstawowego, to jest on wyznaczony wg.:

a.         Formuły Paaschego

 

b.         formuły Fischera

 

c.         formuły Laspeyresa

 

d.         żadna z wymienionych

 

7.  Wskaźnik struktury jest:

 

a.         to stosunek wielkości dwóch zbiorowości będących ze sobą w lo-gicznym związku

 

b.         najczęściej stosowaną (najpopularniejszą) miara klasyczną

 

c.         pozycyjnym współczynnikiem zmienności

 

d.         żadna odpowiedź nie jest prawidłowa

 

8.  Zdarzenie losowe:

 

a.         To zdarzenie pojawiające się przy wykonywaniu doświadczeń losowych,

 

którego wyniku nie można z góry przewidzieć.

 

b.         To samo co doświadczenie losowe

 

c.         Jest to pojęcie pierwotne w rachunku prawdopodobieństwa

 

d.         Należy do zbioru zdarzeń elementarnych

 

 

 

 

9. Dla zdarzenia A’ przeciwnego do zdarzenia A zachodzi zależność:

 

a. A A’ = Ø, oraz     A A’ =

 

b. Żadna odpowiedź nie jest poprawna

 

c. A = A   oraz   A = .

d. Odpowiedzi a i c są poprawne.

 

10.  W urnie znajdują się 3 kule białe i 4 czarne. Losujemy bez zwracania 6 kul, nie sprawdzając ich koloru. Następnie losujemy jedną kule prawdopodobieństwo, że będzie ona biała jest równa:

a. 4/7 b. 1/27 c. 3/4 d. 3/7

 

1.         Które z poniższych nie jest wymagane podczas tworzenia wykresu:

 

a.                       Podanie tytułu wykresu

 

b.     Umieszczenie źródła, z którego zaczerpnięto dane do wykresu

 

c.     Podanie niezbędnych wyjaśnień

 

d.    Umieszczenie wyrazu „miesiąc” lub „rok”, jeżeli na osi y-ków podane są miesiące lub lata.

 

2.         Podstawową metodą opisu współzależności zjawisk jest:

 

a.                       Metoda porównawcza oraz tabelaryczna

 

b.    Odpowiedź a oraz d jest poprawna

 

c.     Metoda agregatowa

 

d.     Metoda graficzna

 

3.         Średnia arytmetyczna jest miarą gorszą od mediany gdy:

 

a.                       Żadna odpowiedź nie jest prawidłowa.

 

b.     Badana zbiorowość jest mniejsza niż 30.

 

c.     Cechy nie mają rozkładu normalnego.

 

d.    Występują obserwacje nietypowe.

 

4.         Kwartyl pierwszy wynosi 10. Oznacza to, że

 

a.                       Dokładnie 75% zbiorowości ma cechę mniejszą bądź równą 10.

 

b.     Mediana jest niższa od średniej arytmetycznej o 10%.

 

c.     Mediana przewyższa średnią arytmetyczną o 10%.

 

d.    Dokładnie 75% zbiorowości ma cechę większą bądź równą od 10.

 

5.         Poniższy szereg określa liczbę psów w rodzinie 0,0,0,1,1,1,22,4,7.

 

Dominantą w tym szeregu jest:

 

a.     0 i 1

 

b.     7

 

c.     0,5

 

d.     W tym szeregu dominanta nie występuje

 

6.         Współczynnik korelacji rang Spearmana:

 

a.                       Można policzyć tylko gdy cechy mają rozkład normalny.

 

b.     Istnieje tylko dla prób o liczbie obserwacji większej niż 100.

c.     Można policzyć także wtedy, gdy cechy mają charakter jakościowy.

 

d.     Tylko dla cech ilościowych

 

7.         Przyrost względny ( ) jest to iloraz przyrostu absolutnego przez:

 

a.                       Tempo wzrostu

 

b.    Wielkość zjawiska z okresu podstawowego

 

c.     Stałą wartość równą 2

 

d.     Wielkość zjawiska z okresu badanego

 

8.         Lista wyników doświadczenia losowego musi spełniać następujący warunek:

 

a.                       Musi być kompletna

 

b.     Elementy listy są parami rozłączne

 

c.     Elementy są nierozkładalne

 

d.    Wszystkie odpowiedzi są poprawne

 

10.     W pierwszej urnie znajdują się 2 kule czerwone i 3 czarne, a w drugiej 1 czarna i 1 biała. Przekładamy (bez sprawdzenia koloru) jedną kule z pierwszej urny do drugiej a następnie losujemy jedną kulę z drugiej urny. Jakie jest prawdopodobieństwo, że wylosujemy kulę czerwoną?

 

a.  3/5

 

b.  3/15

 

c.  2/5

 

d.  2/15

 

 

 

1.  Który ze zbiorowości składa się z jakościowo odmiennych jednostek ? a) próbna

 

b) jednorodna

 

c) niejednorodna d) dynamiczna

 

 

2.  Korelacja jest dodatnia gdy:

 

a)  zmiany obu cech są jednokierunkowe

 

b)  zmiany obu cech są różnokierunkowe

 

c)  sytuacja w której mamy do czynienia ze zbieżnością pojawiania się zdarzeń

 

3. Które zdanie jest prawdziwe:

 

a)  przyrost absolutny pozwala porównać dwie wielkości wyrażone w tych samych jednostkach

 

b)  przyrost absolutny pozwala porównać dwie wielkości wyrażone w różnych jednostkach

 

c)  przyrost absolutny najczęściej używamy do porównań zjawisk w okresach niebezpośrednio następujących po sobie

4.  Jeżeli rozpatrywane zjawiska w czasie są niejednorodne, a chcemy badać zmiany zachodzące w ich wielkościach łącznie, to będziemy posługiwać się:

 

a)  indeksem prostym o stałej podstawie

 

b)  indeksem prostym o zmiennej podstawie

 

c)  indeksem agregatowym

 

d)  indeksem jednopostawowym

 

5.  Który z organów zajmuję się upowszechnianiem wiedzy o statystyce ? a) WUS

 

b) GUS

 

c) Specjalne komórki towarzystw i instytucji naukowo-badawczych d) Resortowe służby statystyczne

 

6.  Wskaźnikiem natężenia, nazywamy:

 

a)  stosunek wielkości dwóch zbiorowości, nie będących ze sobą w logicznym związku

 

b)  liczbową ilustrację udziału poszczególnej części badanej zbiorowości, w całej zbiorowości

 

c)  stosunek dwóch zbiorowości przedstawionych graficznie

 

d)  stosunek dwóch zbiorowości, będących ze sobą w logicznym związku

 

7.  Która z zależności charakteryzuję prawo de Morgana: a) (A ∪ B)' = A' ∪ B'

 

b)  (A ∩ B)' = A' ∪ B'

 

c)  A' ∩ B' = A ∪ B

 

d)  (A ∪ B)' = A' ∩ B

 

8. Iloraz zsumowanych wartości występujących u poszczególnych jednostek nazywamy badanej zbiorowości nazywamy:

 

a)  średnią harmoniczną

 

b)  średnią geometryczną

 

c)  średnią arytmetyczną

 

d)  średnią kwadratową

 

9.  Który z uczonych odpowiada za klasyczną definicję prawdopodobieństwa: a) Laplace

b) Paasche c) Laspeyres d) Kramp

 

10.  Miarą klasyczną jest:

 

a)  mediana

 

b)  kwantyl

 

c)  dominanta

 

d)  średnia kwadratowa

 

1.   Wartość występująca najczęściej w rozkładzie empirycznym cechy to: a) mediana

b) średnia arytmetyczna c) obszar zmienności d) dominanta

 

2.   Miara tendencji centralnej dzieląca zbiorowość na dwie równe części to: a) średnia arytmetyczna

 

b) dominanta c) mediana

 

d) odchylenie standardowe

 

3.   Iloraz zsumowanych wartości występujących u poszczególnych jednostek badanej

 

zbiorowości przez liczbę tych jednostek to:

 

a)  mediana

 

b)  odchylenie standardowe

 

c)  dominanta

 

d)  średnia arytmetyczna

 

4.   Rozstępem (obszarem zmienności) danej cechy mierzalnej jest: a) środek przedziału klasowego

 

b) różnica pomiędzy największą i najmniejszą wartością cechy c) skumulowany rozkład częstości

d) rozpiętość przedziału klasowego

 

5.   Dla szeregu o skrajnej asymetrii prawostronnej:

 

a)  mediana jest mniejsza od średniej asymetrycznej

 

b)  mediana jest większa od średniej asymetrycznej

 

c)  mediana jest równa średniej

 

d)  odchylenie standardowe wynosi 0

 

6.   Miarą klasyczną nie jest a) średnia arytmetyczna b) średnia geometryczna c) mediana

 

d) wariancja

 

7.  W obszarze wartości typowych znajdziemy : a) 33%

 

b) 66% c) 75% d) 99%

8.  Do czego wykorzystamy współczynnik korelacji Pearsona? a) zbadania odchylenia standardowego

 

b) zbadania regresji

 

c) zbadania poziomu korelacji d) wyliczenia wariancji

 

9.  Która z wartość badanej cechy, dzieli populację na dwie części w następujący sposób – 75% jednostek przekroczyło tę wartość, a 25% jednostek jeszcze nie osiągnęło tej wartości:

 

a) średnia arytmetyczna b) kwartyl pierwszy c) mediana

d) kwartyl trzeci

 

10.  Różnica między wielkością zjawiska w okresie badanym a wielkością tego zjawiska w okresie podstawowym to

 

a) Indeks agregatowy b) Przyrost absolutny c) Przyrost względny d) tempo wzrostu

 

**-dobra odpowiedź

 

1.Etapem organizacji badania statystycznego NIE jest:

 

a)przygotowanie badania

 

b)zebranie materiału statystycznego i przygotowanie do opracowania c)prezentacja danych statystycznych d)PODZIAŁ CECH STATYSTYCZNYCH**

 

2.Co to jest grupowanie statystyczne proste?

 

a)ścisłe definiowanie klasy, grupy opierające się na jednej zasadzie grupowania,

 

b)podział badanej zbiorowości ze względu na kilka cech charakterystycznych,

 

c)podział badanej zbiorowości ze względu na jedną cechę charakterystyczną**

 

d)wzajemne wyłączanie się klas, tzn. żaden element nie należy jednocześnie do dwu różnych

 

grup

 

3.Miarą klasyczną jest:

 

a)dominanta

 

b)mediana

 

c)średnia harmoniczna**

 

d)kwantyl

 

4.Miarą pozycyjną dyspersji jest:

 

a)odchylenie przeciętne

 

b)odchylenie ćwiartkowe**

c)odchylenie standardowe

 

d)klasyczny współczynnik zmienności

 

5.Indeksem nazywamy:

 

a)iloraz poziomu zjawiska w okresie badanym do poziomu zjawiska w okresie uważanym za podstawowy**

b)iloczyn poziomu zjawiska w okresie badanym i poziomu zjawiska w okresie uważanym za podstawowy

 

c)sumę poziomu zjawiska w okresie badanym i poziomu zjawiska w okresie uważanym za podstawowy

 

d)różnicę poziomu zjawiska w okresie badanym i poziomu zjawiska w okresie uważanym za podstawowy

 

6.Czym się charakteryzuje korelacja dodatnia?

 

a)zmiany obu cech są różnokierunkowe, a więc wzrost wartości jednej cechy powoduje spadek wartości drugiej

 

b)zmiany obu cech są jednokierunkowe, a więc wzrost wartości jednej cechy powoduje wzrost wartości drugiej**

 

c)zbierznością pojawiania się zdarzeń

 

d)grupowaniem wyników w tablicy korelacyjnej

 

7.Współczynnik korelacji rang Spearmana:

 

a)mierzy liniową zależność między zmiennymi

 

b)mierzy zależność okresową, sezonowość

 

c)jest obliczany w kilkunastu etapach

 

d)pokazuje dowolną monotoniczną zależność (także nieliniową)**

 

8.W zależności od rodzaju związku, funkcje regresjii mogą przybrać postać a)punktową

 

b)liniową lub krzywoliniową**

 

c)kwadratową

 

d)paraboliczną

 

 

 

9.Zbiór zdarzeń elementarnych to:

 

a)dopełnienie wybranego zbioru

 

b)zdarzenie pojawiające się przy wykonywaniu doświadczeń losowych c)zbiór do którego należą wszystkie możliwe wyniki doświadczenia** d)najmniejszy podzbiór wybranego zbioru

 

10.Permutacją bez powtórzeń nazywamy

 

a)każdy n-wyrazowy ciąg, w którym x występuje n razy b)każdy k-elementowy podzbiór tego zbioru

c)każdy n-wyrazowy ciąg utworzony ze wszystkich elementów tego zbioru**

d)liczbę wszystkich różnych ciągów zbioru n-elementowego

 

 

 

 

 

 

 

 

 

 

1.  Co to jest zbiorowość    statystyczna?

 

2.

 

A - jest to zbiór jednostek (osób, przedmiotów lub faktów) podobnych pod względem określonych cech, lecz nie identycznych, objętych badaniem statystycznym.

 

B - Zbiorowość podzielona na klasy według określonej cechy jakościowej lub ilościowej z podaniem liczebności lub częstości.

 

C - uporządkowany według ściśle określonych kryteriów ciąg wielkości statystycznych.

 

D - Zestawienie wyników w postaci szeregu rozdzielczego z cechą mierzalną. Odzwierciedla strukturę badanej zbiorowości z punktu widzenia określonej cechy statystycznej.

 

 

1.  Zbiorowość          statystyczną ze względu na ilość jednostek można podzielić na:

 

A – skończona, nieskończona

 

B – statyczna, dynamiczna

 

C – generalna, próbna

 

D – liczebna, jednostkowa, mieszana

 

 

 

3. Wymień rodzaje materiału statystycznego

 

A – podstawowy, systematyczny, przypadkowy

 

B – liniowy, powierzchniowy, ilościowy

 

C – skumulowany, losowy, cząstkowy

 

D – pierwotny, wtórny, surowy

4. Co to jest wskaźnik natężenia?

 

A – jest to średnia miara wielkości badanego zjawiska

 

B - jest to stosunek wielkości dwóch zbiorowości będących ze sobą w lo-gicznym związku

 

C – jest to stosunek wielkości badanego zjawiska do wielkości czynnika wywołującego to zjawisko

 

D - ilustruje liczbowo udział poszczególnych części badanej zbiorowości w całej zbiorowości.

 

 

 

5. Co to jest miara dyspersji?

 

A – jest to miara służąca wyznaczeniu cechy dominującej w badanej zbiorowości

 

B – jest to miara służąca wyznaczeniu uśrednionej wartości badanej cechy w zbiorowości statystycznej.

 

C - jest to miara służąca do badania stopnia zróżnicowania wartości badanej cechy w całej zbiorowości statystycznej

 

D – jest to sposób wyznaczenia rozpiętości między maksymalną a minimalną wartością badanej cechy

 

 

6. Co to jest korelacja?

 

A- jest to wzajemne oddziaływanie dwóch zjawisk tej samej zbiorowości

 

B – jest to zróżnicowanie pomiędzy maksymalną a minimalną wartością badanej cechy w zbiorowości statystycznej

 

C - jest to podział zbiorowości na mniejsze grupy według kryteriów mających związek z badaniem statystycznym

 

D – jest to sposób analizy informacji dotyczących zbiorowości oraz cech poszczególnych jednostek tej zbiorowości

 

 

7. Wymień rodzaje korelacji

 

A – względna, bezwzględna

B – pierwotna, wtórna, surowa

 

C – dodatnia, ujemna, pozorna

 

D – skokowa, ciągła, quasi ciągła

 

 

 

8. Co to jest przyrost względny?

 

A – średni przyrost zjawiska w badanym okresie czasu

 

B - jest to iloraz przyrostu absolutnego przez wielkość zjawiska z okresu podstawowego

 

C – jest to miara pozwalająca porównać dwie wielkości wyrażone w tych samych jednostkach

 

D – jest to średnia arytmetyczna wyrażona za pomocą wzoru kumulacyjnego

 

 

 

 

 

9. Co to jest index?

 

A - jest to poziom zjawiska w okresie badanym

 

B – jest to tempo zmiany zjawiska statystycznego w badanym okresie

 

C - wielkość badanego zjawiska w okresie podstawowym

 

D – jest to iloraz poziomu zjawiska w okresie badanym do poziomu zjawiska w okresie uważanym za podstawowy

 

 

10.  Z trzech danych elementów: a, b, c, utworzono następujący zbiór par dwuelementowych:

{a, b}, {a,c}, {b, a}, {b, c}, {c, a}, {c, b} jest to:

 

A – wariacja bez powtórzeń

 

B – wariacja z powtórzeniami

 

C – kombinacja bez powtórzeń

 

D – kombinacja z powtórzeniami

1.Ile różnych liczb pięciocyfrowych (cyfry mogą się powtarzać) można utworzyć ze zbioru {1,2,3,4,5} ?

 

A.  250

 

B.  625

 

C.  1250

 

D.  3125

 

2.Cecha mierzalna to:

 

A.  Wykształcenie

 

B.  Narodowość

 

C.  Wielkość zatrudnienia w poszczególnych przedsiębiorstwach

 

3. Zminnością skokową nazywamy:

 

A. Liczbę osób w rodzinie

 

B. Szerokość geograficzną

 

C. Wydatki gospodarsw rolnych

 

D. Wynagrodzenie pracowników

 

4. Zminnością ciągłą nazywamy:

 

A. Liczbę osób w rodzinie

 

B. Szerokość geograficzną

 

C. Wydatki gospodarsw rolnych

 

D. Wynagrodzenie pracowników

 

5. Zminnością quasi ciągłą nazywamy:

 

A. Liczbę osób w rodzinie

 

B. Szerokość geograficzną

 

C. Wydatki gospodarsw rolnych

 

D. Liczba pięter w budynku

 

6.  Jeżęli A jest zdarzeniem losowym oraz A' jest zdarzeniem

 

przeciwnym do zdarzebia A i P(A)=5*P(A'), to prawdopodobieństwo zdarzenia A jest równe

 

A.   4/5

 

B.   1/5

 

C.   1/6

 

D.   5/6

7.     Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczy podzelnej przez 30 jest równe?

 

A.   1/90

 

B.   2/90

 

C.   3/90

 

D.   10/90

 

 

 

8.     Rzucamy dwa razy szęścienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równych trzy wynosi

 

A.  1/6

 

B.  1/9

 

C.  1/12

 

D.  1/18

 

 

 

O zdarzeniach losowych A i Bzawartych w Ωwiadomo, że BA, P(A)=0,7 i P(B) = 0,3. Wtedy

 

A.  P(A∪B) = 1

 

B.  P(A ∪B) = 0,7

 

C.  P(A ∪B) = 0,4

 

D.  P(A ∪B) = 0,3

 

na loterii jest 10 losów,z których 4 są wygrywające. Kupujemy 1 los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe:

 

A.  5/6

 

B.  2/3

 

C.  1/6

 

D.  3/5

 

1.     Organem administracji państwowej przeprowadzającym spisy powszechne jest:

 

a)  Główny Urząd Miar i Wag,

 

b)  Główny Urząd Celny,

 

c)  Główny Urząd Statystyczny,

 

d)  Wojewódzki Urząd Statystyczny.

 

2.     Zbiorowość statystyczna to:

 

a)  zbiór jednostek (osób, przedmiotów, faktów) objętych badaniem,

 

b)  zbiór liczbowy tworzący elementy tego zbioru,

 

c)  zbiór jednostek zawierający tylko cechy mierzalne,

 

d)  wszelkie informacje o każdej badanej jednostce z próby.

 

3.     Zaletą średniej arytmetycznej jest:

a)  jej wartość zawiera się w przedziale <0,1>,

 

b)  jest wielkością obliczalną dokładnie i do obliczenia wykorzystuje się wszystkie dane,

c)  jest konieczna do obliczenia odchylenia ćwiartkowego,

 

d)  informuje o ilości jednostek branych do próby.

 

4.     Przykładem cechy mierzalnej jest:

 

a)  wykształcenie, b) wiek, c) płeć, d) gatunek.

 

5.     W szeregu przeliczalnym punktowym złożonym ze 100 jednostek, wartość pierwszego kwartyla wynosi:

 

a)  75, b) 25, c) 66, d) 50.

 

6.     Miary klasyczne to:

 

a)  wariancja i odchylenie standardowe,

 

b)  odchylenie przeciętne i odchylenie ćwiartkowe,

 

c)  mediana i dominanta,d) kwartyl pierwszy i kwartyl trzeci.

 

7.     Zdarzenie losowe to:

 

a)  zbiór wszystkich parzystych wyników doświadczenia,

 

b)  zbiór wszystkich doświadczeń pochodzących spoza znanego zbioru możliwych wyników,

c)  wyniki danego doświadczenia, których nie można przewidzieć ale mogą być powtórzone,

d)  wyniki danego doświadczenia, które można przewidzieć.

 

8.     Odpowiednikiem zbioru pustego w teorii zbiorów w rachunku prawdopodobieństwa jest:

 

a)  zdarzenie pewne,

 

b)  zdarzenie niemożliwe,

 

c)  różnica zdań,

 

d)  wykluczanie się nawzajem zdarzeń.

 

9.     Podstawowymi pojęciami rachunku prawdopodobieństwa jest:

 

a)  permutacja bez powtórzeń i permutacja z powtórzeniami,

 

b)  zdarzenie losowe,

 

c)  prawdopodobieństwo występowania danego zdarzenia,

 

d)  teoria zbiorów przeciwnych.

 

10.    Do obliczenia wszystkich możliwych permutacji elementów danego zbioru należy zastosować:

 

a)  sumę wszystkich elementów nieparzystych zbioru,

 

b)  Dwumian Newtona,

 

c)  silnię, d) współczynnik korelacji.

 

 

 

 

 

 

            1.1 Podać określenie i przykłady zbiorowości statystycznej generalnej i próbnej.

Zbiorowość statystyczna to zbiór dowolnych elementów (osób, przedmiotów), podobnych pod względem określonych cech (ale nie identycznych) i poddanych badaniom statystycznym.

Zbiorowość generalna: wszystkie elementy będące przedmiotem badania, co do których chcemy formułować wnioski ogólne.

Zbiorowość próbna: podzbiór populacji generalnej, obejmujący część jej elementów (próba).

----------------------------------------------------------------------------------------

1.2 Wymienić rodzaje badań całkowitych i opisać jeden z nich.

Wśród badań całkowitych wyróżnia się:  spis statystyczny, inwentaryzację, rejestrację bieżącą oraz sprawozdawczość statystyczną.

Inwentaryzacja: to spis ujmujący faktyczny stan ilościowy i wartościowy majątku określonej jednostki administracyjnej lub podmiotu gospodarczego.

----------------------------------------------------------------------------------------

1.3 Wymienić rodzaje badań częściowych i opisać jeden z nich.

Wyróżnia się następujące rodzaje badań częściowych:

- badanie reprezentacyjne  - badanie monograficzne  - badanie ankietowe

Badanie monograficzne: polega ono na badaniu indywidualnego przypadku, np. jednego regionu, przedsiębiorstwa czy gospodarstwa domowego, przy czym oprócz charakterystyk liczbowych podaje się też informacje w formie opisowej.

----------------------------------------------------------------------------------------

1.4 Kiedy próba jest reprezentatywna?

Próba jest reprezentatywna kiedy:

-jest wybrana losowo (każda jednostka danej zbiorowości ma znane, różne os zera prawdopodobieństwo znalezienia się w próbie)

- jest dostatecznie liczna

----------------------------------------------------------------------------------------

1.5 Podać różnicę między stymulantą i destymulantą.

Stymulanta to cecha, której wyższe wartości pozwalają zakwalifikować daną jednostkę statystyczną jako lepszą z punktu widzenia realizowanego badania. Destymulanta jest przeciwnością stymulanty ponieważ wysokie wartości świadczą o niskiej pozycji jednostki w zbiorze.

----------------------------------------------------------------------------------------

1.6 Podać po jednym przykładzie stymulanty i destymulanty.

Stymulanta - zarobki ludności w danym regionie podczas badania mającego na celu zbadanie jakości życia w danym regionie.

Destymulanta - skażenie powietrza w danym regionie podczas badania mającego na celu zbadanie zanieczyszczeń powietrz w danym regionie wpływającego na zdrowie i jakość życia mieszkańców.

----------------------------------------------------------------------------------------

1.7 Podać określenie i dwa przykłady cechy skokowej.

Cechy skokowe to takie, które przyjmują skończony lub przeliczalny zbiór wartości na danej skali liczbowej, przy czym najczęściej jest to zbiór liczb całkowitych dodatnich.

np: - liczba osób w rodzinie;  - liczba usterek w wyprodukowanym towarze

----------------------------------------------------------------------------------------

1.8. Podać określenie i dwa przykłady cechy ciągłej.

Cechy ciągłe to takie, które mogą przyjąć każdą wartość z określonego przedziału liczbowego, przy czym liczba miejsc po przecinku jest uzależniona od dokładności pomiaru.

np: -waga danego towaru detalicznego;    - objętość produktu płynnego

----------------------------------------------------------------------------------------

1.9 Dokonać podziału cech statystycznych.                           

Cechy statystyczne dzielimy ze względu na skale pomiarowe i związane z nimi relacje:

- nominalną (relacja: równe lub różne)

-porządkową (relacja: większe lub mniejsze)

-przedziałową ( relacja: większe lub mniejsze)

-stosunkową (relacja: tyle razy większe)

----------------------------------------------------------------------------------------

1.10 Jakie to są cechy mierzalne - podać dwa przykłady.

Cechy mierzalne - właściwości, które można zmierzyć i wyrazić za pomocą odpowiednich jednostek fizycznych (kg. cm. mm itp)

np: - waga produktu badanego;  - wymiary badanej jednostki;

----------------------------------------------------------------------------------------

1.11 jakie to są cechy jakościowe - podać dwa przykłady.

Cechy jakościowe - są to cechy niemierzalne, określane słownie ( płeć, przynależność sektorowa)

np: - mężczyzna;  - inżynier;

 

----------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------

2.1 Definicja szeregu statystycznego.

Szereg statystyczny nazywamy ciąg wielkości statystycznych, uporządkowanych według określonych kryteriów.

----------------------------------------------------------------------------------------

2.2 Podać określanie szeregu rozdzielczego.

Szereg rozdzielczy stanowi zbiorowość statystyczną, podzieloną na części według określonej cechy jakościowej lub ilościowej, z podaniem liczebności lub częstości każdej z wyodrębnionych klas.

----------------------------------------------------------------------------------------

2.3 Jak odróżnić szereg szczegółowy od rozdzielczego.

W szeregu szczegółowym występuje jeden uporządkowany ciąg badanej cechy statystycznej, a w szeregu rozdzielczym występują części (klasy) podzielone według określonej cechy jakościowej lub ilościowej.

----------------------------------------------------------------------------------------

2.4 Jaka jest różnica między wskaźnikiem struktury a wskaźnikiem natężenia?

Wskaźnik natężenia przedstawia wielkość stosunkową wyrażającą kształtowanie się wielkości jednego zjawiska na tle innego. logicznie z nim związanego. Wskaźnik struktury natomiast przedstawia stosunek liczby jednostek o danej wartości cechy do liczebności całej próby.

----------------------------------------------------------------------------------------

2.5 Podać definicję rozkładu empirycznego cechy statystycznej.

Rozkład empiryczny to zestawienie wyników w postaci szeregu rozdzielczego z cechą mierzalną. Odzwierciedla on strukturę badanej zbiorowości z punktu widzenia określonej cechy statystycznej.

----------------------------------------------------------------------------------------

2.6 Jakie wykresy służą do graficznej prezentacji rozkładu empirycznego, gdy dane są w postaci szeregu punktowego?

Wykres słupkowy ( histogramy, wykresy liniowe, diagramy)

----------------------------------------------------------------------------------------

2.10. Wykresem dystrybuanty empirycznej w przypadku danych w postaci szeregu punktowego jest histogram?

histogram

----------------------------------------------------------------------------------------

2.11. Co to jest i jakie wartości przyjmuje wskaźnik podobieństwa struktur ?

Jest miarą stosowaną do pomiaru podobieństwa struktur. Im wartość tego wskaźnika jest bliższa jedności tym struktury badanych zbiorowości są bardziej podobne.

0 < Wp <= 1

----------------------------------------------------------------------------------------

2.12. naszkicować rozkłady : jednomodalny symetryczny, jednomodalny o umiarkowanej asymetrii prawostronnej, rozkład o skrajnej asymetrii lewostronnej.

----------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------

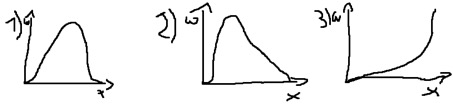
3.1. Wymienić cztery własności średniej arytmetycznej.

-  suma wartości cechy jest równa iloczynowi średniej arytmetycznej i liczebności zbiorowości

- średnia arytmetyczna spełnia warunek:  Xmin < x^ < Xmax

-suma  odchyleń poszczególnych wartości cechy od średniej równa się zero.

-suma kwadratów odchyleń poszczególnych wartości cechy od średniej jest minimalna

----------------------------------------------------------------------------------------

3.2. W jakich przypadkach nie powinno korzystać się z klasycznych parametrów statystycznych?

Wielkości średnich klasycznych zależą od wszystkich wartości przyjmowanych przez cechę w badanej zbiorowości. Jeżeli nie znamy wszystkich wartości nie powinniśmy korzystac z klasycznych parametrów statystycznych.

----------------------------------------------------------------------------------------

3.3 Czym różni się prosta średnia arytmetyczna od średniej arytmetycznej ważonej ?

w średniej arytmetycznej ważonej występują szeregi rozdzielczych punktowych oraz przedziały klasowe. ( tzw.  grupy )

----------------------------------------------------------------------------------------

3.4. Do czego służy współczynnik zmienności ?

Do wyznaczania stopnia zróżnicowania, czyli niejednorodności zbiorowości.

----------------------------------------------------------------------------------------

3.5. Współczynniki zmienności płac w zakładach A i B wynoszą odpowiednio 8% i 15%. Co z tego wynika?

W zakładzie A podane cechy wykazują nieistotne zróżnicowanie statystyczne. W zakładzie B zmienności wynoszą 15% czyli więcej niż 10 zatem zróżnicowanie jest istotone.

----------------------------------------------------------------------------------------

3.6. rozkład dochodów ludności jest prawostronnie asymetryczny. Co to oznacza?

x^ > Mediana > Modalna

----------------------------------------------------------------------------------------

3.7. Rozkład stażu pracy w pewnym zakładzie ma asymetrię lewostronną. Co to oznacza?

x^ < Mediana < Modalna

----------------------------------------------------------------------------------------

3.8. Podać warunki, kiedy można wyznaczyć modalną.

-przedział, w którym występuje modalna oraz dwa sąsiadujące z nim przedziały muszą mieć takie same rozpiętości

- jeżeli rozkłady są wielomodalne obliczanie jednej modalnej jest nieuzasadnione

----------------------------------------------------------------------------------------

3.9. Co to znaczy. że modalna wieku pracowników wynosi 32 lata?

Oznacza to, że wartość cechy statystycznej oznaczającej wiek pracowników, która w danym rozkładzie występuje NAJCZĘŚCIEJ wynosi 32.

----------------------------------------------------------------------------------------

3.10. Wymienić własności mediany.

- może być obliczana w tych przypadkach, w których obliczanie średniej arytmetycznej jest niemożliwe

- mediana nie reaguje na zmiany wartości cech skrajnych

- jeżeli rozkład cechy jest symetryczny to: x^ = Me = Mo

----------------------------------------------------------------------------------------

3.11.Podać interpretacje kwartyla pierwszego i drugiego.

Kwartyl pierwszy: dzieli zbiorowość na dwie części tak, że 25% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu, a 75% równe lub wyższe od niego.

Kwartyl drugi: dzieli zbiorowość na dwie równe części

----------------------------------------------------------------------------------------

3.12. Na czym polega wykres pudełkowy i kiedy go stosujemy?

Na podst wykresu pudełkowego możemy dokonać szybkiej oceny dotyczącej:

-wartości przeciętych

- zmienności

- skośności

- wartości w znacznym stopniu przekraczających przedział zmienności dla wartości typowych

----------------------------------------------------------------------------------------

3.13. Jakich ocen można dokonać na podstawie wykresu pudełkowego.

-wartości przeciętych

- zmienności

- skośności

- wartości w znacznym stopniu przekraczających przedział zmienności dla wartości typowych

----------------------------------------------------------------------------------------

3.14. Podać interpretację przedziału typowych obserwacji.

----------------------------------------------------------------------------------------

3.15. Zakres zmienności obsługi czasu obsługi w okienku kasowym jest określony przedziałem (5min-20min). Co to oznacza?

----------------------------------------------------------------------------------------

3.16. Co to jest wariancja ogólna i kiedy znajduje zastosowanie ?

Jeżeli całą zbiorowość podzielimy według okreslonych kryteriów na r grup, to wariancja dla całej zbiorowości będzie nazywana wariancją ogólną.

----------------------------------------------------------------------------------------

3.17. O czym mówi równość wariancyjna ?

Równość wariancyjna ( wariancja ogólna) mówie o tym, że s^2 = Si^2 + s^2(Xi)

Si^2 - wariancja wewnątrzgrupowa

s^2(Xi) - wariancja międzygrupowa

----------------------------------------------------------------------------------------

3.18. Co określa wariancja międzygrupowa, a co wewnątrzgrupowa ?

Międzygrupowa - wariancja średnich grupowych wartości zmiennej

Wewnątrzgrupowa - średnia arytmetyczna wewnątrzgrupowych wariancji wartości cechy

----------------------------------------------------------------------------------------

3.19. Rozkład wykazuje umiarkowaną asymetrię prawostronną. Jakie nierówności spełniają mediana, modalna i średnia arytmetyczna?

x^ > Mediana > Modalna

 

----------------------------------------------------------------------------------------

3.20. rozkład wykazuje umiarkowaną asymetrię lewostronną. Jakie nierówności spełniają mediana, modalna i średnia arytmetyczna?

x^ < Mediana < Modalna

 

----------------------------------------------------------------------------------------

3.21. Co można powiedzieć o podstawowych miarach położenia, gdy rozkład cechy jest symetryczny?

----------------------------------------------------------------------------------------

3.22. Wymienić dwa przykłady cech statystycznych, dla których korzystny jest rozkład o asymetrii prawostronnej.

- stopień zanieczyszczenia

- ilość osób które chorowały w danym okresie

----------------------------------------------------------------------------------------

3.23. Wymienić dwa przykłady cech statystycznych, dla których korzystny jest rozkład o asymetrii lewostronnej.

- stawka płac

- obroty firmy w zł w danym okresie

----------------------------------------------------------------------------------------

3.24. Oczym mówi kurtoza i jakie wartości może przyjmować ?

Współczynnik skupienia (Kurtoza)

Im większe odchylenie standardowe tym mniejszy współczynnik skupienia.

Im wyższa wartość współczynnika K tym bardziej wysmukła jest krzywa liczebności a zatem większa jest koncentracja wartości cechy wokół średniej.

----------------------------------------------------------------------------------------

3.25. Co to jest linia równomiernego podziału?

----------------------------------------------------------------------------------------

3.26. Co mierzy współczynnik Lorenza i jakie wartości może przyjmować?

KL należy do przedziału ; KL=0 – brak koncentracji, KL=1 – silna koncentracja. Słaba koncentracja jest związana z dośd równomiernym podziałem łącznej wartości badanej cechy pomiędzy jednostki statystyczne opisywane przez daną cechę.

----------------------------------------------------------------------------------------

3.27. Co mierzy współczynnik Giniego i  jakie wartości zwykle przyjmuje ?

Współczynnik Giniego, wskaźnik Giniego, indeks Giniego – stosowana w statystyce miara koncentracji (nierównomierności) rozkładu zmiennej losowej.

·               współczynnik Giniego przyjmuje wartości z przedziału [0; 1], często jednak wyraża się go w procentach

·               wartość zerowa współczynnika wskazuje na pełną równomierność rozkładu

·               wzrost wartości współczynnika oznacza wzrost nierówności rozkładu

·               współczynnik Giniego przyjąłby wartość 1, gdyby tylko jedna obserwacja uzyskała dodatnią wartość zmiennej (na przykład tylko jedno gospodarstwo domowe posiadało dochody) przy nieskończonej liczbie obserwacji

 

----------------------------------------------------------------------------------------

4.1. Podać definicję i przykład zdarzeń losowych.

jeśli E zawiera skończoną lub przeliczalną liczbę elementów, to każdy podzbiór E nazywa się zdarzeniem losowym.

- zdarzenie polegające na wypadnięciu danej liczby oczek w rzucie kostką

----------------------------------------------------------------------------------------

4.2. Zdefiniować i podać przykład zdarzeń wykluczających się.

Zdarzenie V - zdarzenie niemożliwe

Zdarzenie U - zdarzenie pewne

Zdarzenie A i B wykluczają się nawzajem jeśli A(suma)B = V.

----------------------------------------------------------------------------------------

4.3. Jakie warunki określają zdarzenia przeciwne? Podać przykład takich zdarzeń.

Adarzenia A i B są zdarzeniami przeciwnymi, jeśli A(suma)B = U i A(iloczyn)B = V.

Zdarzenia przeciwne sa szczególnym przypadkiem tzw. zupełnego układu zdarzeń.

----------------------------------------------------------------------------------------

4.4 Zdefiniować borelowskie ciało zdarzeń.

Borelowskie ciało zdarzeń Z jest to najmniejszy zbiór podzbiorów przestrzeni E spełniający warunki:

1. U należy do Z

2. V należy do Z

3. suma przeliczalnej liczby zdarzeń należących do Z również należy do Z

----------------------------------------------------------------------------------------

4.5. Kiedy zdarzenia losowe tworzą zupełny układ zdarzeń?

Zdarzenia A1, A2,....,An tworzą zupełny układ zdarzeń jesli Ai (suma) Aj = V dla i != j, i,j = 1, ..., n  oraz A1(suma)A2(suma)....(suma)An = U.

----------------------------------------------------------------------------------------

4.6. Co to jest przestrzeń probabilistyczna?

Przestrzeń zdarzeń elementarnych (E) rozumie się jako zbiór wszystkich niepodzielnych wyników obserwacji czy doświadczenia. Może ona zawierać skończoną lub nieskończoną ilość elementów.

----------------------------------------------------------------------------------------

4.7. Podać klasyczną definicję prawdopodobieństwa.

Jeśli przestrzeń zdarzeń elementarnych E zawiera n jednakowo możliwych zdarzeń elementarnych spośród których Na sprzyjazajściu danego zdarzenia A, to prawdopodobeństwem P(A) zdarzenia A jest  ułamek:

P(A) = n_A / n

----------------------------------------------------------------------------------------

4.8. Wymienić wady klasycznej definicji prawdopodobieństwa.

- możemy z niej skorzystać wtw, gdy mamy do czynienia z przestrzenią E, zawierającą skończoną liczbę zdarzeń elementarnych.

----------------------------------------------------------------------------------------

4.9. Wymienić aksjomaty rachunku prawdopodobieństwa.

1. Każdemu zdarzeniu A (należy) Z można przypisać liczbę P(A), zwaną prawdopodobieństwem zdarzenia A taką, że 0 <= P(A) <= 1

2.Prawdopodobieństwo zdarzenia pewnego równa się jedności tzn P(U) = 1

3. Prawdopodobieństwo sumy skończonej lub przeliczalnej liczby zdarzeń wykluczających się parami równa się smie prawdopodobieństw tych zdarzeń.

----------------------------------------------------------------------------------------

4.10. Podać czestościową (statystyczną) definicję prawdopodobieństwa.

----------------------------------------------------------------------------------------

4.11. Podać definicje i przykład zdarzeń niezależnych.

Jeśli zdarzenia A1, ...An są niezależne to prawdopodobieństwo, że zajdzie przynajmniej jedno z tych zdarzeń, oblicza się, korzystając ze wzoru:

p(A1 (suma) A2 (suma).... (suma) An) = 1 - P  (  A1 (suma) A2 (suma) ... (suma) An  )   <- z kreską ponad ostatnim nawiasem

----------------------------------------------------------------------------------------

4.12. Na czym polega różnica między prawdopodobieństwami a priori i a posteriori?

Prawdopodobieństwo a priori odnosi się do zagadnień dotyczących podejmowania decyzji w warunkach niepewności,a prawdopodobieństwo a posteori dotyczy prawdopodobnieństwa po wystąpieniu zdarzenia A.

----------------------------------------------------------------------------------------

4.13. Ile wynosi prawdopodobieństwo sumy zdarzeń losowych?

P(A(suma)B) = P(A) + P(B) - P(A(iloczyn)B)

----------------------------------------------------------------------------------------

4.14. Jak obliczamy prawdopodobieństwo iloczynu zdarzeń losowych A i B ?

P( A(iloczyn)B ) = P(A) * P(B/A) = P(B) * P(A/B)

----------------------------------------------------------------------------------------

 

51. (11.1) Na czym polega zależność korelacyjna?

Określonym wartościom jednej zmiennej są przyporządkowane ściśle określone średnie wartości drugiej zmiennej.

----------------------------------------------------------------------------------------

54. (11.4)  Co jest miarą siły związku liniowego między cechami statystycznymi?

Współczynnik korelacji liniowej Pearsona przyjmujący wartość od [-1;1] jest miarą związku liniowego między cechami

----------------------------------------------------------------------------------------

56.  Jaki jest związek miedzy siłą zależności korelacyjnej a kątem między prostymi regresji?

Im mniejszy kąt, tym silniejsza korelacja.

----------------------------------------------------------------------------------------

57. Współczynnik korelacji między zmiennymi X i Y wynosi zero. Co z tego wynika w odniesieniu do niezależności czy zależności stochastycznej między tymi zmiennymi?

Oznacza to że X stochastycznie jest niezależny od Y – cechy są nieskorelowane.

----------------------------------------------------------------------------------------

60. O czym mówi współczynnik determinacji, a o czym współczynnik zbieżności?

Współczynnik determinacji informuje nas o tym, w jakim stopniu jedna cecha wyjaśnia drugą. Współczynnik zbieżności odwrotnie, w ilu % (w jakim stopniu)  jedna zmienna nie wyjaśnia drugiej.

----------------------------------------------------------------------------------------

61.  Do czego służy współczynnik korelacji rang Spearmana?

Współczynnik korelacji rang Spearmana służy do opisu siły korelacji dwóch cech w przypadku gdy:

·                   cechy są mierzalne, a badana zbiorowość jest nieliczna,

·                   cechy mają charakter jakościowy i istnieje możliwość ich uporządkowania.

·       ----------------------------------------------------------------------------------------

 

62. (11.12) Co to są empiryczne krzywe regresji zmiennej Y względem zmiennej X?

Empiryczne krzywe regresji zmiennej Y względem zmiennej X powstają przez połączenie punktów o współrzędnych (xi, ўi). Wykres e.k.r pozwala na postawienie hipotezy, że funkcja regresji II rodzaju jest liniowa.

----------------------------------------------------------------------------------------

 

68. Zdefiniować szereg czasowy.

Szereg czasowy to ciąg wyników obserwacji uporządkowanych w czasie, tzn. {t, y_t}; t-jednostka czasu; szereg powstaje w wyniku grupowania typologicznego i wariancyjnego, gdy podstawą grupowania jest zmiana zjawiska w czasie.

----------------------------------------------------------------------------------------

69. Jaki to jest szereg czasowy okresów, a jaki momentów?

Szereg czasowy okresów zawiera informacje o rozmiarach zjawiska w krótkim lub długim okresie czasu, a momentów o rozmiarze zjawiska w danym momencie (np. początek lub koniec miesiąca).

----------------------------------------------------------------------------------------

70. Co to jest trend i jakie są metody jego wyznaczania?

Trend wyraża tendencję rozwojową zjawiska w czasie; wyraża trwałe oddziaływanie szeregu czasowego na wartości Y. W najprostszy sposób przedstawia się go w postaci funkcji liniowej (inne metody: funkcja wykładnicza, potęgowa).

----------------------------------------------------------------------------------------

71.  Co to jest średnia ruchoma i do czego służy?

Prosta średnia ruchoma (krocząca) reprezentuje średni poziom cechy w danym przedziale czasu. Służy do wygładzania szeregu czasowego (częściowo eliminuje wachania okresowe i przypadkowe).

72. Co to są wahania okresowe i jak je dzielimy?

Są to zmiany powtarzające się cyklicznie w mniej więcej tych samych rozmiarach co pewien stały okres czasu. Dzielimy je ze względu na długość na: krótkookresowe, długookresowe.

73. Od czego zależy sposób wyznaczania przeciętnego poziomu zjawiska opisanego szeregiem czasowym.

Od zmian wartości w strukturze ilości i w strukturze cen.

74. Co to jest średnia chronologiczna i kiedy ją wyznaczamy?

Średnią chronologiczną wyznaczamy by policzyć średni poziom zjawiska w przypadku szeregów czasowych momentów. Średnia chronologiczna daje jedynie ogólna orientacje o przeciętnym poziomie badanego zjawiska, bo jest tylko wartością przybliżoną.

76. Do czego służą miary dynamiki o stałej podstawie?

Służą do określania zmiany wartości w okresie T w stosunku do okresu bazowego.

77. Do czego służą indeksy łańcuchowe?

Służą do badania zmiany poziomu zjawiska z okresu na okres.

78. Jakie wartości mogą przyjmować indeksy i jak się je interpretuje?

Gdy indeksy są  w przedziale (0,1) to oznacza spadek wartości, a gdy > 1 wzrost wartości w okresie badanym w stosunku do bazowego/lub poprzedniego. Przyjmują wartości <0,+nieskon.), a wyrażone są w %.

82.O czym mówi równość indeksowa w przypadku indeksów indywidualnych.

i_w= i_p * i_q

Iloczyn indywidualnych indeksów: cen i ilości jest indywidualnym indeksem wartości.

83. Kiedy należy stosować indeksy agregatowe?

Badając dynamikę zespołu zjawisk, gdy produkty są niejednorodne, niesumowalne.

84. O czym mówią agregatowe indeksy cen, a o czym agregatowe indeksy ilości.

Agregatowe indeksy cen – jak zmieniła się wartość produkcji ze względu na zmiany w strukturze cen.

Agregatowe indeksy ilości – jak zmieniła się wartość produkcji ze względu na zmiany w strukturze ilości.

85. Co oznacza agregatowy indeks wartości.

Oznacza zmianę wartości produkcji ze względu na zmiany w strukturze cen i w strukturze ilości łącznie.

87. O czym mówi różnica między licznikiem a mianownikiem w agregatowym indeksie cen Paaschego?

Mówi o tym, o ile zmieniła się wartość w okresie bieżącym w stosunku do podstawowego ze względu na zmiany w cenach.

88. O czym mówi indeks cen przeciętnych i kiedy jest sens go wyznaczać.

Indeks cen przeciętnych, określa jak zmieniła się średnia cena artykułu z powodu zmian w strukturze ilośći z pominięciem asortymentu (gatunku). Stosujemy go by dowiedzieć się jak zmieniła się przeciętna cena w okresie badanym w stosunku do okresu bazowego.

89. Podaj równość indeksową w przypadku indeksów agregatowych.

I_w= _PI_p * _LI_q = _PI_q * _LI_p

90. Co to jest CPI i jak się go wyznacza?

Jest to agregatowy indeks cen, towarów i usług konsumpcyjnych, na którego podstawie oblicza się płacę minimalną, zasiłek dla bezrobotnych oraz inne. CPI = wartość koszyka dóbr i usług w danym okresie/wartość tego samego koszyka w okr. Podstawowym.

91. Podaj interpretację parametrów a i b w funkcji trendu, jeśli wyznaczono ją na podstawie kwartalnych danych.

a – o ile średnio jednostek w kwartale wielkość zjawiska wzrosła (dla a większego od zera) lub zmalała (a mniejsze od 0).

b – oznacza stan zjawiska w ostatnim kwartale roku poprzedzającego badanie (t=0)

93. O czym mówią wskaźniki sezonowości?

Informują nas o tym, o ile procent (lub jednostek – zależy od ujęcia) odchyla się zjawisko od linii trendu.

94. Jaka jest różnica między surowymi i oczyszczonymi wskaźnikami sezonowości?

Oczyszczone wskaźniki sezonowości są to skorygowane wskaźniki surowe, w taki sposób że ich suma jest równa liczbie faz wahań. Suma wskaźników surowych jest bowiem różna od liczby faz wahań.

95. Wymień i opisz składowe szeregu czasowego.

1. Trend wyraża tendencję rozwojową zjawiska w czasie; wyraża trwałe oddziaływanie szeregu czasowego na wartości Y. W najprostszy sposób przedstawia się go w postaci funkcji liniowej (inne metody: funkcja wykładnicza, potęgowa).

2. Wahania okresowe - są to zmiany powtarzające się cyklicznie w mniej więcej tych samych rozmiarach co pewien stały okres czasu. Dzielimy je ze względu na długość na: krótkookresowe, długookresowe.

3. Wahania przypadkowe – występują z różną siłą w różnych kierunkach

 

96. Podaj postać modelu addytywnego szeregu czasowego. Jak go rozpoznać.

Y_t= f(t) + w(t) + z(t)

Model ten cechują liniowa funkcja trendu i w przybliżeniu stała amplituda wahań (efekt piły).

97. Podaj multiplikatywną postać modelu szeregu czasowego.

Y_t= f(t) w(t) z(t)

98. O czym mówi indeks wszechstronny? Np. indeks wszechstronny w analizie płac przeciętnych wyniósł 1,2. Co to oznacza?

Indeks wszechstronny wyraża zmiany w ogólnym średnim poziomie zmiennej ў, które są spowodowane równocześnie zmianami poziomów zmiennych x i z.

99. O czym mówi indeks Paaschego wpływu zmian strukturalnych, a co indeks Paaschego stałej strukturze?

Indeks Paaschego wpływu zmian strukturalnych informuje nas, jak zmieniła się przeciętna płaca w okresie badanym w stosunku do bazowego, jeżli przyjmiemy średnie płace z okresu badanego.

Indeks Paaschego o stałej strukturze informuje nas, jak zmieniła się płaca przy założeniu stałego poziomu i struktury zatrudnienia z okresu badanego.